Parallel and Perpendicular Lines – Explanation
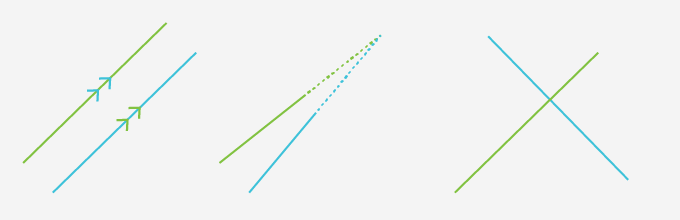
Parallel Lines
Two lines going in a straight path, never intersecting or touching each other, are parallel lines.
Take the below figure, for example, where we have two lines, “a” and “b,” which, as shown, never meet each other.
Image is taken from splashlearn
Properties
Properties of parallel lines are as follows:
- Parallel lines are straight lines.
- Parallel lines have equal distances from each other.
- Parallel lines never meet each other.
- Parallel lines can be extended in any direction.
Transversal
A transversal is a line that intersects two parallel lines.
When it does, many angles are formed, some of them are equal, and others are supplementary.
In the below figure, L1 and L2 are intersected by a transversal, and eight different angles are formed:
Image is taken from splashlearn
- Corresponding angles: Angles that are equal in measure; in the figure above, we can see there are four pairs of corresponding angles which are given below
∠a = ∠e, ∠b = ∠f, ∠c = ∠g, and ∠d = ∠h
- Alternative Interior Angles: Angles are formed inside of two parallel lines and are equal in measure. These angles are given below
∠c = ∠e, ∠d = ∠f
- Alternative Exterior Angles: Angles that are formed on either side of the transversal and in measurement, are equal
∠a = ∠g, ∠b = ∠h
- Consecutive Interior Angles: Supplementary angles which are formed inside of transversal
∠c + ∠f = 180°, and ∠d + ∠e = 180°
- Vertically Opposite Angles: When two lines are equal in measure and intersect each other
∠a = ∠c, ∠b = ∠d, ∠e = ∠g, ∠f = ∠h
Identifying Parallel Lines
Here are some of the characteristics which can help identify parallel lines
- If the Corresponding Angles of two lines are equal.
- If the Alternative Interior Angles of two lines are equal.
- If the Alternative Exterior Angles of two lines are equal.
- If the Consecutive Interior Angles on both sides of the transversal are supplementary.
Parallel Line Equation
Straight Line equation y = mx + b
where “m” is the slope and “b” is the y-intercept, “m” tells us how steep the line is by determining the slope.
Parallel Lines Symbol
Two Parallel Lines are denoted by putting “| |” between the two lines AB and CD as
AB | | CD
Perpendicular Lines
When two lines meet each other at an angle of 90 degrees, they are perpendicular lines.
Image is taken from cuemath
As given in the figure, there are two lines, AB and CD, intersecting at an angle of 90 degrees.
Properties
Perpendicular lines always intersect each other, but all are not perpendicular to each other; if it makes “L” shaped, the angle is a right angle, so the lines are perpendicular.
Some of the properties of perpendicular lines are as follows:
- Perpendicular lines always intersect or meet each other at a right angle.
- Perpendicular lines always make an angle of 90 degrees.
- Two lines which do not cross each other cannot be perpendicular; they are parallel.
Image is taken from splashlearn
- Two lines which intersect each other at acute angles are not perpendicular.
Image is taken from splashlearn
- Any line which is not intersecting at right angles is not perpendicular.
Image is taken from splashlearn
Shapes
Some of the standard mathematical shapes have perpendicular lines:
- Square
- Right-Angled Triangle
- Rectangle
Example
In the given figure, the lines AB and CD are perpendicular (⊥) to each other.
If the given BOC angle is equal to 90 degrees, find the value of x
Image is taken from cuemath
Solution:
First things first, a right-angled triangle can be made or given in any x,y plane; don’t be alarmed if you see it upside down.
BOC = 90°
x + 63° = 90°
x = 90° – 63°
x = 27°
Where x is 27°, if we add both 27° and 63°, we will get an angle of 90° which suggests that the lines are perpendicular to each other.


